In my previous posts on economic and financial concepts, I talked about the idea of a discount rate - the conversion rate between future goods and present goods. But how do you pick a rate to use?
Opportunity Cost
Brian, as you may remember, used the interest rate he had to pay on his debt to help him compare future payments with immediate ones. This is similar to the financial concept of "cost of funding," and it makes some intuitive sense. He can use this to figure out which strategies are strictly better than others.
Abby used the interest rate she earned in her bank account to make the same kind of comparison.
One of these interest rates is the rate you pay on your debt. The other is the rate you earn on savings. Do these seem like different things? To an economist, they're the same.
More precisely, if Abby withdraws $1,000 from her bank account that earns 2% interest per year, then in a year she has $1,020 less in her account. If she borrows $1,000 at 2% interest, then in a year, to pay off the debt she would have to take $1,020 out of her bank account. The amounts are the same for any other time interval too.
Because of this, an economist would say that the interest Abby doesn't earn from the $1,000 she withdrew is a cost, just as much as the interest she would have to pay if she borrowed at that rate. The word for the cost of a foregone opportunity like this is "opportunity cost."
When you think about it this way, Abby and Brian are really doing the same thing when they use the interest rate on Brian's debt, and the interest rate on Abby's savings, to help compare the future with the present. In both cases they are making the comparison by using as their discount rate, the cost of holding onto money, instead paying off debt or putting it into savings.
Picking a Discount Rate Based on Opportunity Cost
You probably have a current "best option" for where to get extra money you need, or where to put extra money. If you have a lot of credit card debt that you have the option of paying off or borrowing more of, then the interest rate on that debt is probably the opportunity cost of doing something else with your money. If you have a lot of savings in the form of mutual funds, then the expected return on your investments is your opportunity cost of doing something else with your money.
A key assumption here is that of "liquidity." Put simply, I'm just talking about cases where you actually can put money into or take it out of something. If you have fixed rate debt that you can't pay off or borrow more from, then there's no decision you can make about that - so it's not a real alternative to other uses for your money.
The world's not always that simple, though. Example:
Dylan has a mortgage with an interest rate of 5%, government savings bonds that earn 6% per year (but new bonds only earn 3%), and an emergency fund in a savings account that earns 0.5%. What should Dylan's discount rate be?
If Dylan has extra money to put somewhere, Dylan's better off paying down the mortgage and "earning" 5% on that money than either buying new savings bonds that earn 3% interest or putting it in the bank account that earns 0.5%. So if Dylan's comparing an option to get money now with an option to get money later, they should use a discount rate of 5%, the interest they can "earn" on that money.
But what if Dylan is comparing a present expense to a future expense? Well, if it's an emergency then Dylan can use the emergency fund to smooth things out. But even then, if Dylan takes their emergency fund seriously, they're going to have to come up with the cash to make up the difference - and that means drawing down those savings bonds (or spending less day to day, but that's a complication I'll get to later). And it's not really practical to borrow a little more against your house every time you have an extra expense. So Dylan's going to have to draw down those savings bonds earning 6%, and that should be Dylan's discount rate for expenses.
A Brief Digression on Interest Rate Arbitrage
Edward has a $100,000 mortgage with an interest rate of 5%, $2,000 of extra money (above what Edward needs for emergencies or to pay ongoing expenses) in a savings account that pays 1% interest per year, and $7,000 of credit card debt with an annual interest rate of 15%. Edward believes that an index fund would grow in value by 6% per year, but hasn't set one up yet. What should Edward do?
Edward has an opportunity to earn some free money here. If Edward takes a dollar from their savings account to pay off credit card debt, the opportunity cost on that dollar is 1% foregone interest per year, but the return on investment is 15% interest Edward won't owe. So on net, just by moving money from one account to another, Edward earns an extra 14%. In general, when one investment is strictly better than another, selling the worse one and buying the better one is called "arbitrage", and this is an example.
So Edward should put as much money as possible into paying off their credit card debt, and put the rest into the investment account. At the end of the process, Edward will have $5,000 in credit card debt, and a discount rate of 15%.
Now let's say Edward gets a $20,000 windfall - an inheritance, a bonus, or a bunch of cash is discovered inside the mattress. What should Edward do?
Well, we know that Edward should first pay off their credit card debt, so that takes care of the first $5,000. But Edward still has $15,000 to invest. What's next?
You can't pay off more credit card debt than you borrowed, so right now Edward has two places to get funds from or put them into: a mortgage with 5% interest and a savings account with 1% interest. You might say that the next best investment Edward has is paying off their 5% mortgage, since Edward "earns" more interest that way than the opportunity cost of 1% interest in the savings account - Edward's getting an extra 4%, free, per year.
But what about the index fund Edward doesn't have?
That's the tricky thing about opportunity cost. You don't just count the opportunities you've taken advantage of in the past - you have to compare all the different options you have now. Edward expects a 6% annual return on shares in an index fund. So the opportunity cost of doing anything else is 6%. From that perspective, Edward would actually be losing 1% in interest each year on any money used to pay off that 5% mortgage ahead of schedule.
The best choice for Edward is to open up an investment account and use the remaining $15,000 to buy shares in that index fund. Edward's return on investment is 6%, so that's the discount rate Edward should use when comparing other future and present payments and expenses.
Indifference Curves
Let's say I want to buy some fruit for a snack. $1 will buy me an apple, or an orange. I like them both about the same, so I'm indifferent between these choices. If either of them only costs $0.90, I'll buy that one.
But I have a strong preference for more tastes in a meal. Suppose the store's running a special where for $1 you can get half an apple and half an orange. I'm going to get this. I'd even spend more than $1 on it.
Economists call this a "revealed preference" that I put the same value on one apple or one orange, but a higher value on the first half of each.
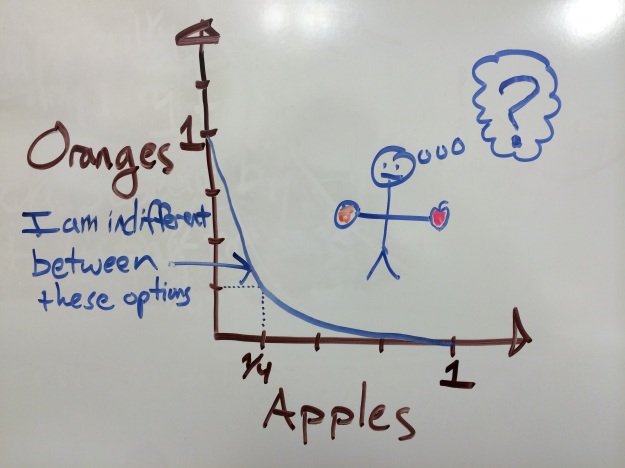
That's not very interesting yet, but let's say the combination is just a quarter of an apple and a quarter of an orange, still for $1. Now I'm torn again - I could go for either the orange, the apple, or the combo.
Since apples and oranges can be divided nearly continuously, you could describe a mathematical curve of the apple-orange combinations I'd be indifferent between. This is called an "indifference curve."
You can draw more than one indifference curve. The curve that passes through the quarter-apple and quarter-orange combo isn't the same curve that passes through the halfsies combo - I prefer any point along the second curve to any point along the first curve.
If your preferences are consistent, no two indifference curves will ever intersect. So if you prefer 10 hats to 5, and 10 scarves to 5, your indifference curves can't look like this:
If those were your utility curves, then you'd prefer 10 hats to 5 hats, and you'd be indifferent between 5 hats and a combination of 3 1/3 hats and 3 1/3 scarves, and you'd be indifferent between that combination and 10 hats. (Of course, you can't really have a third of a hat in any meaningful way. Economic reasoning often assumes that quantities are continuous, which is rarely completely true, but often close enough to be useful.)
Indifference curves tell you what you already know, but they don't help you extend your knowledge beyond the examples you think through. We want something that will help us abstract what we learn from our indifference curves, and apply that knowledge to many cases at once. That's why utility functions exist.
Utility Functions
Economists basically pretend that your indifference curves are a side effect of your attempts to maximize some mathematical function of the things you consume. In the case of my snacktime decision, I am trying to buy the combination that maximizes some function U=f(n_apples, n_oranges) subject to my budgetary constraints.
In this model, an indifference curve is just the set of all points with the same utility U - if they're all worth the same amount of utility, I don't care which one I pick - I'm indifferent. But if choices are on different indifference curves, that's the same as saying that they have different amounts of utility - and I'll always try to pick the one with a higher value of U.
Let's take a simple example and imagine that I'm indifferent between one orange, one apple, and half of each, and that I prefer any of two oranges, an orange and an apple, or two apples - but am indifferent between that set as well. In that case, my indifference curve is just a straight line, and my utility function is:
U=f(n_apples,n_oranges)=1*n_apples+1*n_oranges.
If I set U=1, I get:
1=n_apples+n_oranges
n_oranges=1-n_apples
This produces my first indifference curve.
If I set U=2, I get:
2=n_apples+n_oranges
n_oranges=2-n_apples
This produces my second indifference curve.
One important point here is that since utility is a quantity we can't observe directly, and we only observe the direction of a preference, not the strength of that preference, it doesn't matter if I'm maximizing U or 1,000,000*U or U+1,000,000. I make the same decisions in any of those cases. So as a quantity, utility is meaningless, but it explains the existence of indifference curves very simply.
Now let's talk about discount rates again.
Using Indifference to Infer a Discount Rate
Discount rates are ways of comparing valuable things in the future to valuable things in the present. (I used money because it's a simple example, but you may have time preferences about other things.)
So one thing you can do is assume that you have some fixed discount rate of x%, and ask yourself, would you rather eat a chocolate bar tomorrow, or 1.5 chocolate bars next year? (Don't ask about right now, because of hyperbolic discounting.) Adjust the amounts up or down until you get quantities where you're conflicted about the choice. Then you have an estimate of your true discount rate.
You should probably try comparing several kinds of valuable things, at several time scales, to get your true discount rate - your intuitions won't all be perfectly consistent, and you're trying to get something that's a good approximation for most of your preferences, not just your preferences about the first example you think of.
Would I rather spend an extra day hanging out with a friend this year, or two extra days with a friend in ten years?
Try to come up with some more examples on your own. Then you can back out your discount rate from your indifference curves, and pick a rate in the middle of your estimates.
Here's how to back out a rate. Let's say I'm indifferent between eating 20 chocolate truffles this week, and 21 chocolate truffles in a year. That's one year of discounting, so my rate is just 21/20 - 1 = 1.05 - 1 = 0.05 = 5%
On the other hand, let's say that I'm indifferent between spending a day with a friend this year, and two days in ten years. I need to back out the annual discount rate from that. I'll do it using a computer, I'm to lazy to use logarithms, but it's not particularly hard math if you want to look up how to do it yourself:
(2/1)^(1/10) - 1 = 1.07 - 1 = 0.07 = 7%
So I decide my subjective discount rate's about 6%.
What if My Discount Rates Don't Agree?
If your subjective discount rate is lower than your financial discount rate, then you're generally better off saving money and spending it later. Some people report that when they reflect for long enough on their subjective discount rates, they don't want to discount at all. Those people should only spend money now on things if they compound over time better than financial investments (like some education, spending time with friends, repairing their car so they can get to work, or relaxation so they don't have a breakdown between now and retirement) and things that will be much less enjoyable later in life (your gear to climb Mount Everest won't do you any good when you're 90 years old and can't get out of bed without help, even if it's much more affordable for you then).
If your subjective discount rate is higher than your financial discount rate, then you might be saving too much. That doesn't mean you should spend everything now, since your discount rate is a marginal rate that can change as you move money from the future to the present.
There are two complicating factors:
1) I mentioned hyperbolic discounting above. Basically this is when pleasure and pain in the extremely short term feels like it vastly outweighs much larger amounts of pleasure or pain even the moderately near future. Most people don't endorse their own hyperbolic discounting, and there's no point in using a clever theory to do things you don't actually prefer by blowing all your money on one wild night in Vegas.
2) Declining marginal utility - this is basically a way of expressing the fact that I'd rather have an orange every day of the year, than 365 oranges today and none for the next 364 days. Your subjective discount rate isn't absolute, and it's going to be affected by how satisfied you already expect to be in the present vs. the future. If you alter this by transferring money from present you to future you or vice versa, your discount rate will change. Because of this, you may not even want to bother with a subjective discount rate - use your opportunity cost discount rate to make sure you're making consistent decisions, and comparing equivalent quantities of present vs. future stuff. Use discounting to make consumption decisions on a case-by-case basis, and notice if it always seems like a good idea to move things in one direction.



Pingback: Is Veganism Correct? | Compass Rose
Pingback: Is Veganism Correct? | Effective Altruism Society of DC